APUNPORTES Beler Nolasco: Tarea evaluable T2

Situación

Unos investigadores desarrollan un nuevo entorno virtual de aprendizaje basado en Google Apps. Para evaluar la incidencia de la utilización de este nuevo entorno en las calificaciones de los estudiantes, durante dos años se realiza un estudio de caso con dos grupos de estudiantes: un grupo de control que utiliza Moodle y un grupo experimental que utiliza Google Apps.

Que se pide

Para cada uno de los años, analizar si existen diferencias estadísticamente significativas entre las calificaciones de ambos grupos.

El registro del caso se recoge en los siguientes ficheros:

CARGAR DATOS

Cargar segundo archivo

NOTA

EL SEGUNDO ARCHIVO ESTA DIVIDIDO POR SIGNO DE # POR LO QUE COPIAMOS EL CODIGO DE LA RUTA Y EN SEP AGREGAMOS EL SIGNO UTILIZADO EN ESTE ARCHIVO, de lo contrario nos dará error.

Notas.2grupos.v2 <- read.delim("C:/Users/pc/Desktop/TAREA OSKAR2/Notas-2grupos-v2.csv", sep = "#")

Figura 1.0

ANALIZAREMOS SI EXISTE DIFERENCIAS ESTADÍSTICAMENTE SIGNIFICATIVAS ENTRE LAS CALIFICACIONES DE AMBOS GRUPOS, POR AÑOS.

Despejamos las variables que vamos a utilizar

Primer año

> datosMoodleaños1 <- subset(Notas.2grupos.v1, grupo =="Moodle")

> datosGoogleappsaños1 <- subset(Notas.2grupos.v1, grupo =="Google Apps")

Figura 1.2

Segundo año

> datosMoodleaño2 <- subset(Notas.2grupos.v2, grupo =="Moodle")

> datosGoogleappsaños2 <- subset(Notas.2grupos.v2, grupo =="Google Apps")

figura 1.3

Ejecutamos el t.test

Comparando de la siguiente manera

GRUPO AÑO 1	GRUPO AÑO 2
datosMoodleaños1---------->	datosMoodleaño2
datosGoogleappsaños1----à	datosGoogleappsaños2

Media de las notas de los estudiantes que utilizaron Moodle año 1 y Moodle año 2.

Figura 1.4

¿Qué nos indican los resultados?

En primer lugar, que la media de la variable x (datosMoodleaño1$nota) es de 6.25, mientras que la variable y (datosMoodleaño2$nota) tiene una media de 6.55, para una diferencia de -0.3 Por tanto, como hemos dicho anteriormente, la diferencia entre ambos grupos no parece significativa porque es tan sólo de -0.3.

¿Es esta diferencia ESTADÍSTICAMENTE significativa? Es decir, ¿la diferencia se debe al factor diferencial entre ambos grupos o se debe al azar? Para saberlo, nos fijamos en el p-value.

¿Qué indica el p-value? Indica que el riesgo a equivocarnos al afirmar "Si, existe una diferencia estadísticamente significativa entre ambos grupos debida al factor diferencial entre dichos grupos", cuando en realidad dicha diferencia no se debe al factor diferencial entre grupos, sino al azar. En este caso, p-value = 0.4577 = 45% ose, un error muy grande de equivocarnos.

Figura 1.5

Como vemos, en lo que respecta a la calificación final, el riesgo que corremos al afirmar "Sí, existe una diferencia estadísticamente significativa entre ambos grupos determinada por la plataforma utilizada en cada grupo" es grande.

Media de las notas de los estudiantes que utilizaron Google Apps año 1 y Google Apps año 2.

Figura 1.6

¿Qué nos indican los resultados?

Podemos observas que los estudiantes que utilizaron google apps, tanto el primer año como el segundo no reflejaron ninguna a diferencia estadísticamente hablando debido a que la media obtenida son iguales tanto para x(7.25) como para y(7.25) y nuestro margen de error p-value = 1

Figura 1.7

p-value en estadística

¿Qué es un valor p?

Utilice el valor p para determinar si los resultados son estadísticamente significativos. Los valores p suelen utilizarse en las pruebas de hipótesis, donde usted rechaza o no puede rechazar una hipótesis nula.

Cuando usted realiza una prueba de hipótesis, el elemento clave de la salida en el que hay que concentrarse es el valor p.

Un valor p oscila entre 0 y 1. El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.

Puede comparar el valor p con el nivel de significancia (α) para decidir si debe rechazar la hipótesis nula (H₀).

Si el valor p es menor que o igual a α, rechace H₀.

Si el valor p es mayor que el nivel de significancia (α), usted no puede rechazar H₀.

Para el nivel de significancia (α) suele utilizarse un valor de 0.05, entonces, si el valor p es menor que o igual a 0.05, rechace H₀.

Ahora analizaremos los datos de la siguiente manera

Veremos si existe alguna diferencia estadística cuando los estudiantes en un año utilizaron
Moodle un año y Google Apps otro año.

Moodle año 1 vs Google Apps año 2 y Google Apps año 1 vs Moodle año 2

GRUPO AÑO 1	GRUPO AÑO 2
datosMoodleaños1------------------>	datosGoogleappsaños2
datosGoogleappsaños1--------------->	datosMoodleaño2

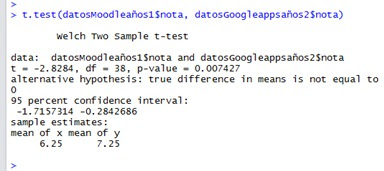
t.test(datosMoodleaños1$nota, datosGoogleappsaños2$nota)

Figura 1.8

¿Qué nos indican los resultados?

para los estudiantes que el primer año utilizaron Moodle y el siguiente año Google Apps En lo concerniente a la media x (6.25) y (7.25), podemos observar que existe un crecimiento en la nota de los estudiantes. de una diferencia de 1.

el p-value =0.007427, nos dice que tenemos un margen de equivocarnos sí afirmamos que esto se debió al alzar de 0,07%, en pocas palabras sí podemos afirmar que se debió al azar, puesto que se encuentra por debajo del 5%.

Figura 1.9

t.test(datosGoogleappsaños1$nota, datosMoodleaño2$nota)

Figura 2.0

¿Qué nos indican los resultados?

Para el caso de los estudiantes que utilizaron el primer año Google Apps y el segundo año Cambiaron a Moodle tenemos una media de x(7.25) mientas que para y(6.55) con una disminución de la nota al pasar de Google Apps a Moodle. nuestro p-value =0.08832 para un 8,831999999999999 %, concluyendo que no se debió al azar sino, a la diferencia de grupo.

Conclusiones

Podemos concluir diciendo que las calificaciones varían para mejoría, utilizando el entorno Google Apps, pero esto no representa una diferencia estadística significativa.

En el caso de la figura 1.6 donde la media en ambos casos tienen un valor de 7.25, del análisis de Google Apps año 1 y Google App año 2, podemos decir que no se figura variación en las notas.

Fuentes Bibliográficas
http://www.mutae.net/2016/01/bt01-bt02-actividad-9-introduccion-r.html
https://cran.r-project.org/doc/contrib/rdebuts_es.pdf