Unos investigadores desarrollan un nuevo entorno virtual de aprendizaje
basado en Google Apps. Para evaluar la incidencia de la utilización de este
nuevo entorno en las calificaciones de los estudiantes, durante dos años se
realiza un estudio de caso con dos grupos de estudiantes: un grupo de control
que utiliza Moodle y un grupo experimental que utiliza Google Apps; el reparto
de sujetos entre ambos grupos se realiza siguiendo un criterio de paridad de
sexo.
SE PIDE:
1.
Observar los datos y reflexionar acerca
de la relación que existe entre las variables calificación, grupo y sexo.
2.
Dibujar en Excel o Google Sheets un
gráfico de interacción (http://courses.washington.edu/smartpsy/interactions.htm) de las medias de
las calificaciones combinando las variables grupo y sexo, es decir:
Moodle-Male, Moodle-Female, GoogleApps-Male, GoogleApps-Female. ¿Coinciden los
resultados mostrados en el gráfico con tus reflexiones del apartado
anterior?
3.
Analizar si existen diferencias
estadísticamente significativas en las calificaciones en función del grupo y
del sexo.
4.
Utilizar la función aov() de R para saber
si existe una interacción estadísticamente significativa entre las variables
grupo y sexo.
1. Observar los datos y
reflexionar acerca de la relación que existe entre las variables calificación,
grupo y sexo.
 |
| Figura 1.0 |
Abrimos
la interfaz R studio y cargamos el fichero de datos desde la cuadrícula
superior derecha: Import Dataset → From text file
 |
| Figura 1.1 |
A continuación se abre
una ventana en cuya parte derecha se muestra, por un lado, el contenido del
fichero de texto que deseamos cargar, y por otro lado, la estructura de datos
que se va a cargar en R a partir de dicho contenido según las opciones indicadas
en la parte izquierda de ventana. Para que la creación de la estructura de
datos se realice de forma correcta, debemos indicar a través de dichas opciones
si el contenido del fichero de datos incluye una cabecera, cuál es el separador
utilizado entre variables, cuál es el carácter utilizado para separar la parte
entera de la parte decimal de un número, etc.
 |
| Figura 1.2 |
 |
| Figura 1.3 |
Si el proceso se realiza correctamente, la estructura de datos debería
aparecer representada en una nueva cuadrícula. El entorno queda compuesto
de 4 cuadrículas: la cuadrícula superior derecha se utiliza para cargar datos y
visualizar las variables de trabajo; la cuadrícula superior izquierda se
utiliza para visualizar el contenido de dichas variables; la cuadrícula inferior
izquierda se utiliza para introducir los comandos para procesar y analizar los
datos; y la cuadrícula inferior derecha se utilizar para visualizar gráficas.
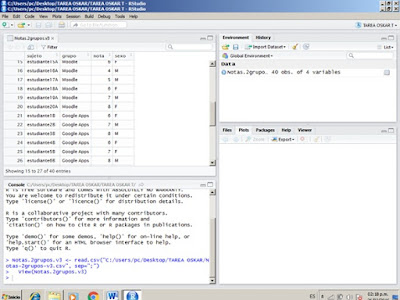 |
| Figura 1.4 |
Los siguientes
pasos van dirigidos a la obtención de
los siguientes grupos de datos a partir del primer archivo: Moodle-Male,
Moodle-Female, GoogleApps-Male, GoogleApps-Female. En dicha figura se
diferenciarán, mediante distintos colores, los estudiantes entorno sexo
FILTRADO DE DATOS
Para filtrar los sujetos
por tipo entorno, escribimos los siguientes comandos en la consola:
grupoMoodle <- subset(Notas.2grupos.v3, grupo=="Moodle")
grupoGoogleApps <- subset(Notas.2grupos.v3, grupo=="Google Apps")
Al ejecutar estos comandos, se crearán dos nuevas variables: grupoMoodle y grupoGoogleApps.
 |
| Figura 1.5 |
Para filtrar los sujetos por tipo de entorno y sexo, escribimos los
siguientes comandos en la consola:
oodle-Male <- subset(grupoMoodle, sexo==”M”)
Moodle-Female <- subset(grupoMoodle,
sexo==”F”)
GoogleAppMale <- subset(grupoGoogleApps,
sexo=="M")
GoogleappsFemale <-
subset(grupoGoogleApps, sexo=="F")
Al ejecutar estos comandos, se crearán cuatro nuevas variables: oodle-Male, Moodle-Female, GoogleAppMale
y GoogleappsFemale.
 |
| Figura 1.6 |
En este punto tenemos la división por sexo, grupo y
calificaciones al mismo tiempo.
ANÁLISIS REFLEXIVO
Observando detenidamente cada
grupo ordenados o agrupados de la siguiente manera ( Moodle.Male, Moodle.Female, GoogleApp.Male
y Googleapps.Female) podemos
visualizar a simple vista que no existe ninguna relación aparentemente
significativa, ya que las notas en la mayoría de casos guardan similitudes en
ambos grupos tomando en cuenta el sexo, como lo hemos hecho en este caso.
2. Dibujar
en Excel o Google Sheets un gráfico de interacción (http://courses.washington.edu/smartpsy/interactions.htm) de las medias de las calificaciones
combinando las variables grupo y sexo, es decir: Moodle-Male, Moodle-Female,
GoogleApps-Male, GoogleApps-Female. ¿Coinciden los resultados mostrados en el
gráfico con tus reflexiones del apartado anterior?
En el siguiente proceso
analizaremos la media de cada grupo atendiendo
a su sexo
Creamos los grupos GrupoMoodle y GrupoGoogleApps
Con los siguientes códigos:
GrupoMoodle
<- subset(Notas.2grupos.v3, grupo =="Moodle")
GrupoGoogleApps
<- subset(Notas.2grupos.v3, grupo =="Google Apps")
 |
| Figura 2.0 |
Luego agrupamos por sexo cada grupo con
los siguientes códigos
GoogleApps.Male <- subset(GrupoGoogleApps, sexo
=="M")
GoogleApps.Female <- subset(GrupoGoogleApps,
sexo =="F")
Y
Moodle.Male <- subset(GrupoMoodle, sexo
=="M")
Moodel.Female <- subset(GrupoMoodle, sexo
=="F")
 |
| Figura 2.1 |
ANÁLISIS DE DATOS.
En primer lugar, debemos de obtener los valores del análisis en cada categoría
para luego realizar nuestros gráficos de interacción.
Primero buscaremos los datos
estadísticos, tomando en cuenta la calificación o nota por grupo y por sexo con
la siguiente línea de códigos:
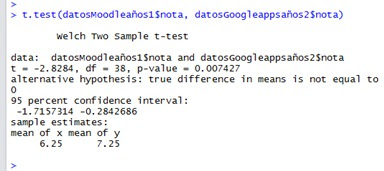
t.test(grupoGoogleApps$nota, grupoMoodle$nota)
RESULTADOS
Análisis de datos por grupo
(GrupoGoogleApps vs GrupoMoodle)
 |
| Figura 2.2 |
ANÁLISIS DE DATOS POR SEXO
Moodle.Female$nota vs GoogleApps.Female$nota
 |
| Figura 2.3 |
 |
| Figura 2.4 |
Veamos algunos gráficos de interacción de los datos de las figuras 2.2, 2.3 y 2.4.
GoogleApps
|
Moodle
|
7.25
|
5.25
|
Moodle.Female
|
GoogleApps.Female
|
5.9
|
6.6
|
Moodle.Male
|
GoogleApps.Male
|
4.6
|
7.9
|
|
|
3. Analizar si existen diferencias estadísticamente significativas en las calificaciones en función del grupo y del sexo.
- Haciendo referencia a la figura 2.2 la cual analiza en función de los grupos Moodle y Google Apps, donde tenemos una media en x=7.25 y=5.25 y un p-value = 1.683e-06 encontramos que se encuentra muy por encima del margen de error de 5%.
- La figura 2.3 nos referencia en el análisis de Moodle.Female y GoogleApps.Female donde obtuvimos un media de x=5.9 y=6.6 y un p-value = 0.1069 para un 10% de margen de error.
- Para la figura 2.4 tenemos la siguiente media x=4.6 y=7.9 con un p-value=2.603 para un margen de error muy alto.
De los tres casos anteriores podemos sacar las siguientes conclusiones:
Existe un margen de error muy grande al afirmar que es debido al azar y no al factor diferencial del grupo.
Que los estudiantes con la media mas alta corresponden a los Google App.
4. Utilizar la función aov() de R para saber si existe una interacción estadísticamente significativa entre las variables grupo y sexo.
resultados.aov <- aov(nota~(grupo*sexo), data =Notas.2grupos.v3)
> summary(resultados.aov)
Df Sum Sq Mean Sq F value Pr(>F)
grupo 1 40.0 40.00 47.06 5.02e-08 ***
sexo 1 0.0 0.00 0.00 1
grupo:sexo 1 16.9 16.90 19.88 7.74e-05 ***
Residuals 36 30.6 0.85
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 |
| Figura 2.5 |